Ray casting is a technique widely used in 3D environments. It consists in casting a “ray” from a given position in a given direction. The algorithm will then tell you things like where a collision happened, what was the normal of the surface, etc. In this article, I will describe a way of implementing a similar technique in a 2D tile-based environment. Implementing this technique in your game engine can give you benefits like pixel-perfect collision detection.
Download the .NET / C# source code
Download the .NET demo
For this article, I won’t go into the details for loading or drawing a 2D scene. I will focus on the 2D ray casting technique. All the code described here can be found in the Scene and Tile classes.
The Tile class
To implement this technique, our Tile class will need to have two main properties: Bitmap and SolidityMap. The Bitmap property simply contains the graphic representation of the tile. The SolidityMap property is a 2D array which will tell us which part of the tile is solid and which is not. This array can be built from the bitmap using the alpha value of each pixel – if the pixel is transparent, it can be crossed, otherwise it’s solid (Fig. 1).

Figure 1: Tile bitmap and solidity map.
public class Tile {
private Bitmap bitmap;
private bool[,] solidityMap;
public void BuildSolidityMap() {
solidityMap = new bool;
for (int x = 0; x < bitmap.Width; x++) {
for (int y = 0; y < bitmap.Height; y++) {
// if the pixel is not transparent set
// the solidity map value to "true"
solidityMap[x, y] = bitmap.GetPixel(x, y).A != 0;
}
}
// We will need some additionnal processing here if the tile is
// transformed in some way
// (like horizontally or vertically flipped)
// This code is in Tile.cs
}
public bool[,] SolidityMap {
get { return solidityMap; }
}
public Bitmap Bitmap {
get { return bitmap; }
set { bitmap = value; }
}
}
Checking if a pixel can be crossed or not
Before doing any ray casting, we need to be able to find out if a given pixel of the scene can be crossed by a ray. I won’t go into the details as it is now quite obvious how to implement it using our SolidityMap property:
// Find out if the given pixel is traversable.
// X and Y are the scene pixel coordinates
public bool IsPointTraversable(int x, int y) {
// Get the tile coordinates from the pixel coord.
int tileX = (int)Math.Floor((float)x / (float)tileSize);
int tileY = (int)Math.Floor((float)y / (float)tileSize);
// If the point is out of bound, we assume it's traversable
if (tileX < 0) return true;
if (tileX >= horizontalTileCount) return true;
if (tileY < 0) return true;
if (tileY >= verticalTileCount) return true;
Tile tile = GetTile(tileX, tileY);
// If the tile is blank the point is traversable
if (tile == null) return true;
// Get the coordinates of the point within the tile
int localPointX = x % tileSize;
int localPointY = y % tileSize;
// Return "true" if the pixel is not solid
return !tile.SolidityMap[localPointX, localPointY];
}
Casting a ray using the Bresenham algorithm
The core of our ray casting functions will be the good old Bresenham algorithm, which after 44 years is still the fastest way to plot a (non-antialiased) line from A to B. There are plenty of resources on the net to implement it. Here I’ve chosen to implement the optimized version described on Wikipedia. The function takes two points as input, and will return the list of all the points crossed by that line. This function is not completely optimized – it would be better to calculate in advance the number of points the line will contain so that we can use a fixed-size array instead of a list. It should improve the speed quite significantly, especially for the longer lines. Anyway, here is the function:
// Swap the values of A and B
private void Swap<T>(ref T a, ref T b) {
T c = a;
a = b;
b = c;
}
// Returns the list of points from p0 to p1
private List<Point> BresenhamLine(Point p0, Point p1) {
return BresenhamLine(p0.X, p0.Y, p1.X, p1.Y);
}
// Returns the list of points from (x0, y0) to (x1, y1)
private List<Point> BresenhamLine(int x0, int y0, int x1, int y1) {
// Optimization: it would be preferable to calculate in
// advance the size of "result" and to use a fixed-size array
// instead of a list.
List<Point> result = new List<Point>();
bool steep = Math.Abs(y1 - y0) > Math.Abs(x1 - x0);
if (steep) {
Swap(ref x0, ref y0);
Swap(ref x1, ref y1);
}
if (x0 > x1) {
Swap(ref x0, ref x1);
Swap(ref y0, ref y1);
}
int deltax = x1 - x0;
int deltay = Math.Abs(y1 - y0);
int error = 0;
int ystep;
int y = y0;
if (y0 < y1) ystep = 1; else ystep = -1;
for (int x = x0; x <= x1; x++) {
if (steep) result.Add(new Point(y, x));
else result.Add(new Point(x, y));
error += deltay;
if (2 * error >= deltax) {
y += ystep;
error -= deltax;
}
}
return result;
}
Finally, the actual ray casting function
The RayCast() function will perform the ray casting. The ray will be cast from a given Position in a given Direction, and with the specified RayLength (Fig. 2), and will return a RayCastingResult class to allow us to handle the collision in the game.
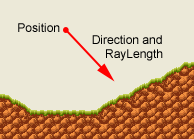
Figure 2: Position, Direction, and RayLength parameters
// Class returned by the RayCast() method
public class RayCastingResult {
// Does the ray collide with the environment?
private bool doCollide;
// And if so, at which position?
private Vector position;
public bool DoCollide {
get { return doCollide; }
set { doCollide = value; }
}
public Vector Position {
get { return position; }
set { position = value; }
}
}
In the RayCast() method, we will start by retrieving the list of all the points crossed by the ray using the Bresenham algorithm:
List<Point> rayLine = BresenhamLine(position,
position + (direction.GetNormalized() * rayLength));
Then, we will loop through all these points, starting from the specified position, for the whole length of the ray or until we find the collision point. Once we find that point, we exit the loop and return the RayCastingResult instance.
while (true) {
Point rayPoint = rayLine[rayPointIndex];
if (!IsPointTraversable(rayPoint.X, rayPoint.Y)) {
result.Position = Vector.FromPoint(rayPoint);
result.DoCollide = true;
break;
}
For more details, here is the full RayCast() method:
public RayCastingResult RayCast(Vector position,
Vector direction, float rayLength) {
RayCastingResult result = new RayCastingResult();
result.DoCollide = false;
// Exit the function now if the ray length is 0
if (rayLength == 0) {
result.DoCollide = IsPointTraversable((int)position.X,
(int)position.Y);
result.Position = position;
return result;
}
// Get the list of points from the Bresenham algorithm
List<Point> rayLine = BresenhamLine(position,
position + (direction.GetNormalized() * rayLength));
if (rayLine.Count > 0) {
int rayPointIndex = 0;
if (rayLine[0] != position) rayPointIndex = rayLine.Count - 1;
// Loop through all the points starting from "position"
while (true) {
Point rayPoint = rayLine[rayPointIndex];
if (!IsPointTraversable(rayPoint.X, rayPoint.Y)) {
result.Position = Vector.FromPoint(rayPoint);
result.DoCollide = true;
break;
}
if (rayLine[0] != position) {
rayPointIndex--;
if (rayPointIndex < 0) break;
} else {
rayPointIndex++;
if (rayPointIndex >= rayLine.Count) break;
}
}
}
return result;
}
Performance
Doing this kind of pixel-perfect ray casting might seem a bit over kill, however, I found it’s usable and fast in a game environment when used reasonably. The most important is to use the ray length parameter properly, and to set it to the minimum possible value. For instance, if over a frame, a bullet is moving from A to B, don’t cast a ray through the whole scene, but instead limit the length of the ray to |B-A|.
In most cases, the ray is going to cross several empty tiles (which translates to many quick tile == null tests). Once we find a non-empty tile, in the worst case, we will have 23 values to test in the SolidityMap array (for 16×16 pixel tiles). The only case when it might be a problem is when trying to cast a long ray in a scene with tiles with many holes (Fig. 3). But again, setting the ray length to a proper value should get rid of the problem.

Figure 3: Worst case scenario. None of the tiles crossed by the ray is empty, and they all have a big hole in the middle.